Decentralized underwriting

An Insurance DAO (iDAO) is a DAO devoted to the work of underwriting insurance policies. An iDAO consists of member underwriters who sell insurance policies to non-member customers, creating a decentralized underwriting market. Tokenomics formulas give numerical estimations for premia pricing as a function of risk which predicts valuations for the market and the likelihood of iDAO ruin, which dictates the capital reserves required for an iDAO.

iDAOs under DGF can be more efficient than traditional insurance companies, since REP tokens in an iDAO can serve as substitutes for capital reserves depending on the degree of decentralization of the iDAO.

Overview

Insurance is essential for every type of business transaction, every type of property, every type of service engaged in business. Every type of economic action is made more efficient when decisions are hedged, so we can be more confident in our investments in the future. Such stability allows more complex business arrangements which exploit subtler opportunities for profit. To achieve this stability, we require the trust that transactions will finalize satisfactorily as planned, or in the event of unforseen failure, that the contract will be made whole by the platform running the marketplace.

Therefore insurance is an essential industry for the modern economy. Like the appeals process of the law, like policing, like the effort to keep track of reputation and maintain the protocols of governance, insurance is also an overhead cost that does not directly generate profit. It’s a type of business cost that any efficiency-minded engineer would prefer to eliminate entirely. But inasmuch as we can’t predict the future, insurance will never be eliminated, because it is valuable. Insurance improves the efficiency of the economy by investing in the future, to guarantee the system will continue running, despite inevitable unforeseen problems. Insurance mitigates risk. Insurance helps people overcome the fear of joining a business transaction due to the risk of loss. In physics jargon, insurance is a business catalyst, which provides activation energy for a transaction.

Decentralized insurance requires networks of policy writers with individual reputations for efficient underwriting of every type of transaction. In the basic iDAO workflow detailed below, which follows the basic DGF workflow, there are three crucial but unintuitive steps:

1. An underwriter gets new REP, instead of cash from premia, for selling contracts.
2. All premia are given to the entire iDAO (REP salary), not the underwriter who risks REP.
3. A claim is paid by a REP market which auctions the particular underwriter’s REP tokens. Underwriter loses REP, not money directly. And the risk is not covered by the entire iDAO, but only the specific underwriter who issues the contract.

Insurance DAO protocols

Components

1. iDAO = {Underwriters}
2. Underwriter ∋ REP tokens
   • Propose contracts with REP
   • Police contracts with REP
3. Insurance contract (Work smart contract)
4. Validation Pool
5. REP-to-BOND market

Token scheme

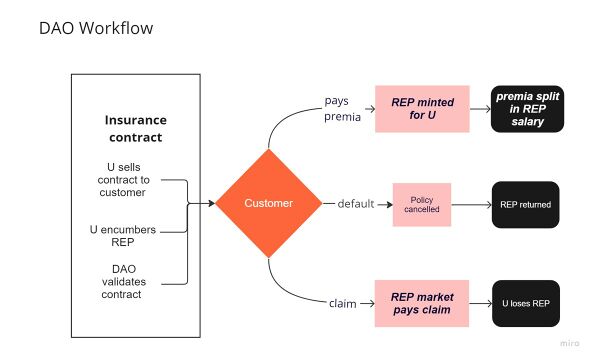
The following basic workflow illustrates how an iDAO creates REP tokens and distributes premium cash money from customers.

Workflow

(See Figure 1.)

1. Underwriter $U_{1}$ sells a contract to a customer.
2. $U_{1}$ encumbers the canonical amount of REP in the contract.
3. Contract Validated by DAO.
4. Customer
   • pays premia, or
   • defaults, or
   • claims
5. iDAO
   • mints REP for $U_{1}$ proportional to premia & distributes REP salary, or
   • cancels contract, or
   • pays claim by burning encumbered REP and minting sufficient BONDs to cover the claim (REP-to-BOND market)

Figure 1: iDAO workflow follows basic DGF workflow iterated each time a premium is paid

Notes:

• If a customer makes a claim on the policy, the contract governs how the claim is validated. Typically an oracle and an adjudicator are necessary for this step, which are outside the scope of this specification.
• If a claim is validated, the underwriter's encumbered REP is auctioned at market to pay the claim.
  • If the auction price of the encumbered REP is sufficient to cover the claim, and excess cash or REP from the auction is returned to the underwriter.
  • If the auction price of the encumbered REP is insufficient to cover the claim, further REP is minted and sold at market until the claim is covered. Any excess cash from this process is donated to the iDAO's capital reserve.
• In practice, an iDAO would likely give members the opportunity to keep their REP tokens if the underwriter covers the claim personally. In such cases calling the BOND market would be unnecessary. This would be an attractive choice for most active underwriters, since REP tokens have greater powers than BOND tokens.
• The REP-to-BOND market is designed to prevent a 51% attack. When a claim is made, the REP encumbered in the insurance contract is burned. Then BOND tokens, which have no governmental power in the DAO, are minted in sufficient quantity to cover the claim. BOND tokens pay off in the future through the REP salary. Through this mechanism a 51% attack is inhibited and the iDAO is strengthened, because only those underwriters who prove competent at issuing insurance contracts according to the standards of the iDAO are given REP power.

Properties engendered

• More transparent than traditional insurance companies, therefore an iDAO can be continually audited, and so may be more trustworthy
• More stable because risk is more decentralized and diversified
• More meritocratic (rewards and punishment are more isolated on the active underwriter)
• Democratized access to participation at all levels
• Incentivizes policing since all members suffer if a contract is insufficiently covered by encumbered REP
• Group doesn’t suffer directly when a claim is made (except loss of future premia). Loss is limited to the underwriter who wrote the contract. In fact, weak underwriting skills is naturally discouraged, since underwriters who choose untrustworthy customers will automatically lose their REP stake.
• Capital reserve holdings can be securely decreased (see below), since the market covers more value than traditional premium pricing models which rely on immediate premium inflows.

• ZK proofs allow the insured to share more information without sacrificing privacy. This minimizes adverse selection, leading to more accurate actuarial approximation of probability of loss, which leads to more efficient markets for coverage, which is better for both the insurers and the insured.

Tokenomics

Insurance DAO valuation

In this section, we value REP tokens in an iDAO.

Components

1. iDAO $=\{Underwriters\}=\{U_{i}\}=$ ledger of all REP tokens
2. $C(t)=$ Capital reserves
3. $\{active\ contracts\}=\{+\ premia\}\cup \{-\ risk\ of\ potential\ claims\}$  

Following basic tokenomics formulas, we make the following definitions:

1. $R(t)=$ the total number of REP tokens in the iDAO at time $t$.
2. The rate of total premia $f'={df \over dt}$ that the iDAO earns. Therefore $f(t)$ denotes the total fees earned from the beginning of the iDAO until time $t$.
3. $f_{0}^{1}(t)$ is the cumulative reputational salary collected for one REP token.
4. $m$ is the minting ratio.
5. $r$ is the base discounting rate.
6. $L$ is the lifetime after which a REP token expires.

Fundamental results

The basic results of REP tokenomics give the present value of a single REP token with finite lifetime $L$. Theorem 3.  (Finite Life Tokens)

The total number of active REP tokens at any time $t$ is

$$R(t)=\int _{t-L}^{t}m*f'(s)ds.$$

The premia REP salary fees it earns is given by

$$f_{0}^{1}(t)=\int _{0}^{min\{t,L\}}{\frac {f'(s)}{R(s)}}ds.$$

Assuming an iDAO has exponentially growing fees $f'(t)=f_{0}'e^{ct}$ and risk is always covered accurately by the REP market, then after the iDAO has been running $L$ units of time, the number of active REP tokens will grow at a proportional exponential rate. The income stream of a single token is then

$$f_{0}^{1}(t)={\frac {c}{m(1-e^{-cL})}}min\{t,L\}$$

with present value

$$PVf_{0}^{1}={\frac {1}{m}}{\biggl (}{\frac {1-e^{-rL}}{rL}}{\biggr )}{\biggl (}{\frac {cL}{1-e^{-cL}}}{\biggr )}$$

Actual fees are stochastic, not exponential. $f(t)$ is a random variable. So accurately valuating REP is a difficult problem for the market, which depends on the set of all active contracts, health of the marketplace (actuarial statistics), and history of the DAO and the talent of its underwriters in selling contracts. The larger and more decentralized the market, however, the more predictable $f(t)$ becomes.

Basic theory of premium pricing makes

$$f\propto \Pi _{X}=E(X)(1+\theta )$$

using the simplest pricing principle where ${\textstyle \Pi _{X}}$ is the price of the contract which covers risk ${\textstyle X}$ which is a random variable given by a claim. ${\textstyle \theta }$ is the premium loading factor, which contains the extra transaction costs that an underwriter demands in order to issue a contract.

Capital reserves

A capital reserve in a traditional insurance company is a treasury of liquid cash set aside for future insurance liabilities, to cover all risk beyond the present period’s premia collection. The size of an iDAO's capital reserve holdings is an important issue. If the reserve is too small, the risk of insolvency and ruin is unreasonable. If the reserve is too high, the holding costs of the liquid cash increases the costs of insurance.

For an iDAO insurance contract, when a claim is made, money to cover the claim can be taken from two sources:

1. iDAO treasury of capital reserves
2. REP-to-BOND market. (The encumbered REP tokens are burned and equivalent BONDs are minted and sold at market for immediate cash to cover the claim. If enough REP was encumbered at the point the contract was sold and validated by the DAO, then there is no problem. If it wasn’t enough, then the treasury is necessary, or more BONDs needs to be minted, which diminishes all members’ REP value.)

This second source of coverage for claims gives a new twist on classical ruin theory: The treasury is completely unnecessary if there are enough fees coming in to guarantee the future value of REP is sufficient for the REP-to-BOND market to cover the claim.

Capital reserve holdings are a contentious issue in traditional economics. Traditional regulatory agencies such as the BIS, IMF, the Fed, and the World Bank have had differing regulatory standards at different times in history (Bretton Woods Agreement, e.g.) to manage different types of risk. After a global meltdown, regulation tightens. After a decade of security, regulations loosen. This leads to cycles of security crises. Economists don't have any complete model for authoritatively answering how large a capital reserve should be, since there are many competing variables which hold differing explanatory capacity in differing market circumstances. But traditional economies enjoy the advantage of regulators with asymmetric information and power. A central bank can manipulate their interest rates or reserve holdings standards with greater freedom than a DAO. Those regulators do not need to justify or publish their reasoning.

Web3 DAOs, on the other hand, demand far more explicit and more rigorous regulatory rules than traditional firms, because of their openness to pseudonymous members, their open source operating procedures, and their transparent financial transactions. Fortunately, the algorithmic execution of smart contracts in open decentralized platforms gives an unprecedented level of transparency which leads to more perfect markets, which leads to greater predictability. Information asymmetry is minimized. Further, transaction costs are diminished with electronic self-execution of smart contracts. Further, decentralization encourages diversity, which promotes deep and fluid markets, leading to greater stability.

In an iDAO, the size of the capital reserves does not need to cover 100% of estimated risk, because there is also the value of the equity stock in the company and its market inertia (i.e., its history of fair business even after temporary random setbacks). This is part of the reason theoreticians often conclude an insurance firm should cover 100% of risk with capital reserves, but in practice, laws in certain insurance realms only require 8-12% of the risk to be covered with the reserve. The value of the company in that case, will itself cover the other ~90%. We know the company would refinance in case of temporary difficulties. The company would be willing to take a loan to cover debt for the opportunity to continue working and insuring people after a temporary setback. The proof that the company is willing and capable of covering claims even when they are temporarily in the hole gives greater promise of future cash flows, which usually outweighs the debt.

This gap has not been investigated properly. Older companies may deserve to enjoy the gap in full coverage, but younger companies with less track record and less talent and inertia will not deserve the same gap—they should be collateralized 100%. Such regulation should explicitly include that valuation of the company formulaically, not with discrete jump standards imposed by slow governmental bureaucracies.

What makes this obvious in our case is how REP is a hybrid financial tool with 3 functions:

1. REP is equity since it gives claims on future DAO profits through the REP salary.
2. REP is also a utility token, because it is required to participate in new underwriting.
3. REP tokens are essential to the process of covering claims, so it is constantly revaluated through the REP market.

The amount of reserves necessary is dependent on incoming fees (as usual) and future value of existing REP tokens as equity (based primarily on existing contracts and secondarily on the history of the DAO—it’s long-term reputation for doing business, proving it has accumulated talent) and as utility. So, as long as underwriters are doing their jobs, there is then less need for reserves. How much less?

It depends on the existing contracts relative to the quantity of active REP and the risk of those contracts being claimed or defaulting. That depends on many factors, such as the current health of the systems being insured as measured by actuarial statistics and historical inertia. The short answer is, we don’t know. We don’t really know how much an insurance company is worth because of the large amount of risk it covers. It has a high variation, depending on how many premia the iDAO will earn in the future.

However, if we can get a good estimate on the future premia the iDAO will collect, then we can have more confidence in the precise relation between the size of reserve and the risk of iDAO ruin. We make this relation clear below, by formulating the explicit dependence on the increase or decrease of premia.

So we need to trust the estimate of the future direction of the rate of premia in the DAO. If the market does not have enough inertia and decentralization to diversify the risk, giving enough stability to value the company above 0 for a long enough time to cover its contracts, then an iDAO will require a reserve which guarantees full coverage.

In general, if the fees are stable or increasing faster than interest/inflation $r$, and faster than the valuation at the initiation of a contract, then the tokens are worth more than the estimate and no reserve is necessary assuming the DAO is policing the contracts properly (i.e., the proper amount of REP was encumbered in all contracts to cover the risk). Conversely, if fees are decreasing, then a reserve may be necessary to prevent a death spiral. So the amount of capital reserves necessary is greater when fees are decreasing faster than predicted at the moment the contracts were valuated. In sum, the size of the reserve required is smaller when the rate of fees are increasing and larger when the rate decreases. This is partially a positive feedback cycle, because if you drop the reserve in good times, then need to save in bad times, that is difficult. Building the reserve when REP is losing its value might lead to the increased perception that REP loses its value. However, that is not correct, because a REP token is a claim on the reserve they are building. So existing REP doesn’t really lose value by building a reserve. It just delays the reward, and loses the relatively minor opportunity cost of holding the liquid cash in reserve for future claims during down periods.

Strangely, if the public loses confidence in the DAO and stops paying premia, then the risk is decreased, since the previous valuations of the encumbered REP are decreased by the loss of premia, but the contracts that defaulted were under-encumbered, so the defaults decrease the risk exposure of the DAO. Any new contracts underwritten with REP can be achieved with the usual market update of the value of REP.

So when premia are decreasing that shrinks the value of REP. The amount of value that the REP loses by fair valuation according to the tokenomics formulas, times the amount of REP encumbered in risky contracts, needs to be covered by depositing the remaining premia in reserve, to the degree that all existing contracts can be covered. Then the iDAO will die if all fees go into the reserve and all the reserve is claimed. In that case the underwriters will lose all their REP value, but the customers would all be covered. That is fair, because that would mean every single contract was claimed, which means the underwriters did a terrible job and deserve to lose their REP. However, that is statistically unlikely in a large DAO. Whoever didn’t have a customer claim on the contracts the underwriter wrote, then the underwriter still has REP and so still has a claim on the remaining reserve, and can still underwrite new contracts or cash out. So the iDAO will continue to live as long as a single underwriter is still doing their job.

This all assumes the market is predictable, which relies partially on the present value formula being predictable. The reserve needs to build when the fees are decreasing and the reserve can shrink and reward underwriters through the REP salary when fees increase. (E.g., increased claims can sometimes decrease the fees, if the insured cancel their policies, or if they are dropped by underwriters who don’t want to continue to insure them, or if underwriters increase their fees.)

So the 0th order state is if the DAO values the contracts properly based on the evidence they have for REP value, then it the DAO remains sound. If they underestimate or overestimate the value, the DAO should build or shrink the reserve—1st order adjustments. 2nd order adjustments may eventually be merited if the DAO become large and stable enough for the measurements to be accurate enough to overcome stochastic errors.

What happens if everyone claims their policy at the same time when a reserve is gone? Then the DAO defaults on the claims, because no one will be getting fees, so the REP will be worthless. So we need to assume the REP market is valuable.

There are more issues that can be explored. For example, if there is an increased demand for insurance, as measured by an increase in contracts, which is reflected in an increase in premia and therefore an increase in the REP salary, then the DAO profits increase which means the salary increases. However, since more REP will be minted, a single REP token may not increase in value. [??check against tokenomics formulas.] Based on this, existing contracts may be over-encumbered (or under-encumbered if premia decrease or the market dips). How should we respond? Governance can be made to adjust the requirements based on those market forces.

Quantifying the relation between reserves and risk of ruin

We can use the basic tokenomics formulas to make a precise relation between the size of reserve holdings and the risk of an iDAO defaulting on its customers' claims.

??No, the following analysis is flawed. An iDAO defaulting is independent of how many or few claims, since exposure is limited to the particular underwriters. The iDAO will only default if the previously established value of REP decreases while the group is exposed to risk, in which case the DAO would need to mint more BONDs to cover the excess risk. We need to compare the change in REP value from decreasing premia. So we make an assumption of a certain equilibrium amount of premia (equivalent to picking a value for REP tokens, though the different contracts will have different quantities of REP with different values at different contract initiation points. So we simplify, by assuming all contracts had a short enough negotiation time to assume the REP value in all contracts is the same. That all risk C was covered at that time, but now the premia have dropped. Now what is the relationship between K and the probability of iDAO ruin? Then we can show how exponential P' assumptions can be correlated with changing K to keep the probability fixed. ??

The probability of default

$$Pr_{C}(default)=Pr(T_{K,f}<\infty )=\lim _{t\to \infty }Pr(T_{K},f<t)$$

is the probability that the stopping time

$$T_{K,f}:=inf\left\{t:K(t)+\int _{t}^{\infty }e^{-r(s-t)}P'(s)ds>\int _{t-1}^{t}C'(s)ds\right\}$$

is finite. Here 1 is the unit of time which represents 1 period of the BOND market. The term$\int _{t-1}^{t}C'(s)ds$ represents the amount of claims made since the previous BOND market period. The term $\int _{t}^{\infty }e^{-r(s-t)}P'(s)ds$ is the value of the BOND market at time $t$.  We want to capture the idea that at this time the claims might exceed the value of the market, which would lead to a collapse in the value of REP and the ruin of the iDAO if the capital reserve  is insufficient to cover the difference.

Evidently, the probability of ruin depends on the

Economic analysis

We compare this decentralized scheme with the traditional insurance model, analyzing the microeconomics of supply and demand, moral hazards and adverse selection.

Where we stand practically in deFi

Missing:

• Oracles are not decentralized and efficient
• Adjudication
• Stable coins are not decentralized and/or efficient
• Smart contracts are not efficient
• Local legal regulatory clarity is mostly non-existent

See Also

• BONDs
• Fixed period BONDs
• Graceful Exit BOND market